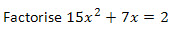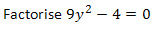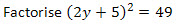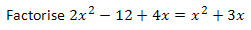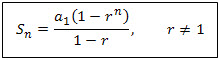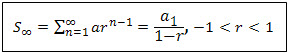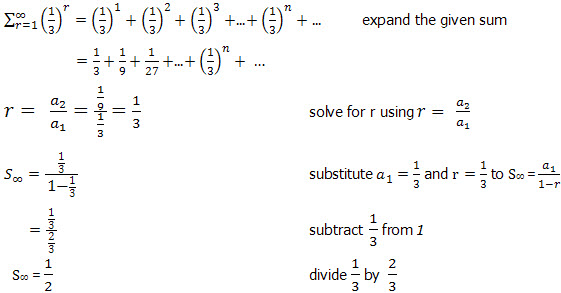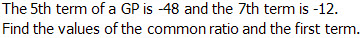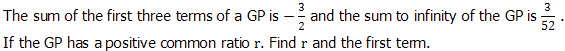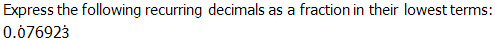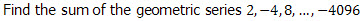Geometric Progression, Series & Sums
Introduction
A geometric sequence is a sequence such that any element after the first is obtained by multiplying the preceding element by a constant called the common ratio which is denoted by r. The common ratio (r) is obtained by dividing any term by the preceding term, i.e.,
| where | r | common ratio |
| a1 | first term |
| a2 | second term |
| a3 | third term |
| an-1 | the term before the n th term |
| an | the n th term |
The geometric sequence is sometimes called the geometric progression or GP, for short.
For example, the sequence 1, 3, 9, 27, 81 is a geometric sequence.
Note that after the first term, the next term is obtained by multiplying
the preceding element by 3.
The geometric sequence has its sequence formation:
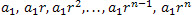
To find the nth term of a geometric sequence we use the formula:
| where | r | common ratio |
| a1 | first term |
| an-1 | the term before the n th term |
| n | number of terms |
Sum of Terms in a Geometric Progression
Finding the sum of terms in a geometric progression is easily obtained by applying the formulas:
nth partial sum of a geometric sequence
sum to infinity
| where | Sn | sum of GP with n terms |
| S∞ | sum of GP with infinitely many terms |
| a1 | the first term |
| r | common ratio |
| n | number of terms |
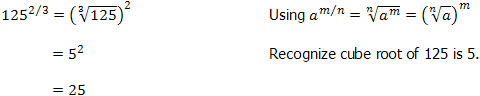
Examples of Common Problems to Solve
Write down a specific term in a Geometric Progression
Question
Write down the 8th term in the Geometric Progression 1, 3, 9, ...
Answer
Finding the number of terms in a Geometric Progression
Question
Find the number of terms in the geometric progression 6, 12, 24, ..., 1536
Answer
Finding the sum of a Geometric Series
Question
| Find the sum of each of the geometric series | 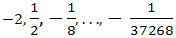 |
Answer
Finding the sum of a Geometric Series to Infinity
Question
Answer
Converting a Recurring Decimal to a Fraction
Decimals that occurs in repetition infinitely or are repeated in period are called recurring decimals.
For example, 0.22222222... is a recurring decimal because the number 2 is repeated infinitely.
The recurring decimal 0.22222222... can be written as
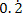
.
Another example is 0.234523452345... is a recurring decimal because the number 2345 is repeated periodically.
Thus, it can be written as
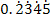
or it can also be expressed in fractions.
Question
Express
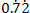
as a fraction in their lowest terms.
Answer
Try this question :
Question 1

Question 2

Question 3
Question 4
Question 5
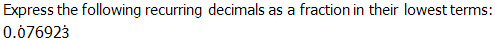
Question 6
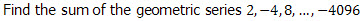
Question 7

Question 8